有些几何最值问题，几何变量关系不明显，需要挖掘变量之间关系，通过恰当设取恰当未知数，让学生求出变量间的函数表达式，然后再让学生求变量的最值，这类问题需要用函数模型解决，但是也有很多几何最值问题并没有给出求函数表达式的指令，所以很多学生想不到，对于此类问题，更多学生往往不知道应该选择何种模型，所以应当重视这类问题。

建立函数模型求最值一般需要以下几个步骤：

（1）选择自变量，确定自变量的取值范围；

（2）求得函数解析式；

（3）在自变量取值范围内利用配方或函数图象的最高点（或最低点），二次函数需结合顶点公式，求得函数的最大值（或最小值）.

1．（2019秋•嘉兴期末）一副三角板（△ABC与△DEF）如图放置，点D在AB边上滑动，DE交AC于点G，DF交BC于点H，且在滑动过程中始终保持DG＝DH，若AC＝2，则△BDH面积的最大值是（）

A．3B．3√3C．3/2D．3√3/2

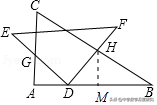
【解析】：本题考查了二次函数的性质，解直角三角形，三角形全等的判定和性质以及三角形面积，得到关于x的二次函数是解题的关键．

如图，作HM⊥AB于M，∵AC＝2，∠B＝30°，∴AB＝2√3，

∵∠EDF＝90°，∴∠ADG+∠MDH＝90°，

∵∠ADG+∠AGD＝90°，∴∠AGD＝∠MDH，

∵DG＝DH，∠A＝∠DMH＝90°，

∴△ADG≌△MHD（AAS），∴AD＝HM，

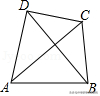
2．（2019秋•松滋市期中）如图，四边形ABCD的两条对角线互相垂直，AC+BD＝16，则四边形ABCD的面积最大值是（）

A．16B．32C．36D．64

【解析】：设AC＝x，四边形ABCD面积为S，则BD＝16﹣x，

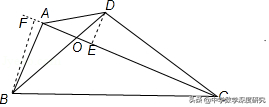
当x＝8时，S最大＝32；

所以AC＝BD＝8时，四边形ABCD的面积最大，故选：B．

变式．（2019•无锡模拟）四边形的两条对角线AC、BD所成的锐角为45°，当AC+BD＝9时，四边形ABCD的面积最大值是（）

A．75√2/4B．81√2/16C．19√2D．21√2

【解析】：过点B作BF⊥AC，与CA延长线交于点F，过点D作DE⊥AC于点E，∵AC与BD所成的锐角为45°，∴BF＝OBsin45°，DE＝ODsin45°，

∴四边形ABCD的面积S＝

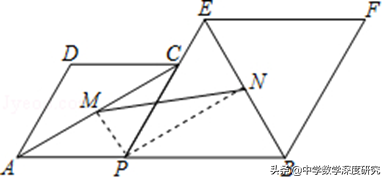
3.（2019•顺庆区校级自主招生）如图，已知AB＝8，P为线段AB上一个动点，分别以A、B为边在AB的同侧作菱形APCD和菱形PBFE，点P、C、E在同一直线上，∠DAP＝60°，M、N分别是对角线AC、BE的中点．当点P在线段AB上移动时，线段MN的最小值是_____．

【解析】连接PM、PN．首先证明∠MPN＝90°设PA＝2a，则PB＝8﹣2a，PM＝a，PN＝√3（4﹣a），构建二次函数，利用二次函数的性质即可解决问题；连接PM、PN．

∵四边形APCD，四边形PBFE是菱形，∠DAP＝60°，

∴∠APC＝120°，∠EPB＝60°，

∵M，N分别是对角线AC，BE的中点，

∴∠CPM＝1/2∠APC＝60°，∠EPN＝1/2∠EPB＝30°，

∴∠MPN＝60°+30°＝90°，

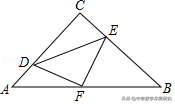
4．（2019春•雁塔区校级期末）如图，在等腰Rt△ABC中，∠C＝90°，AC＝8，F是AB边上的中点，点D、B分别在AC、BC边上运动，且保持AD＝CE，连接DE、DF、EF，则△CDE面积的最大值为______．

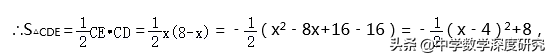
【解析】设AD＝x，则CE＝AD＝x，CD＝8﹣x，根据三角形面积公式列式，由二次函数配方可得最大值．

∵﹣1/2＜0，∴当x＝4，即AD＝4时，△CDE面积有最大值是8，

故答案为：8．

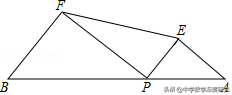
5．（2019•晋江市一模）如图，点P为线段AB（不含端点A、B）上的动点，分别以AP、PB为斜边在AB的同侧作Rt△AEP与Rt△PFB，∠AEP＝∠EPF＝∠PFB＝90°，若AE+PF＝8，EP+FB＝6，则线段EF的取值范围是_______．

【解析】本题考查二次函数最值，三角形相似，勾股定理，平行线的判定，是综合性很强的一道题；能够通过平行得到三角形相似，能够通过相似得到边的关系，利用勾股定理得到二次函数的解析式，再由二次函数的值的范围求解，因此熟练掌握相似、平行、二次函数最值的求法是解题的关键．

解一（函数思想）：设AE＝x，PE＝y，则PF＝8﹣x，BF＝6﹣y，

∵∠AEP＝∠EPF＝∠PFB＝90°，∴PE∥BF，∴△PEA∽△BFP，

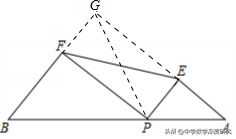
解二（几何思想）：延长BF、AE相交于点G，连接GP，

∵∠AEP＝∠EPF＝∠PFB＝90°，∴四边形GFPE是矩形，∴FE＝GP，

∵GF＝PE，GE＝BF，∴BG＝BF+PE，AG＝AE+FP，

∵AE+PF＝8，EP+FB＝6，

∴BG＝6，AG＝8，∴AB＝10，

当GP⊥AB时，GP最小，最小值为24/5；

当EF与GA重合时，EF最大，最大值为8，

∵点P为线段AB（不含端点A、B）上的动点，∴24/5≤EF＜8．

故答案为故答案为24/5≤EF＜8．

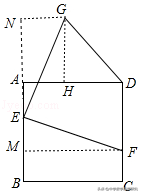
6.如图，正方形ABCD的边长为2，点E、F分别是边AB、CD上的动点，且AE＝CF，连接EF，将线段EF绕点E逆时针旋转90°得到线段EG，连接DG，则线段DG长的最小值为_______

【解析】：如图，过点F作FM⊥AB于M，过点G作GH⊥AD于H，GN⊥AB于N，∵四边形ABCD是正方形，

∴AB＝BC＝AD＝CD＝2，∠B＝∠C＝∠BAD＝90°，

且FM⊥AB，GH⊥AD，GN⊥AB，

∴四边形BCFM，四边形AHGN是矩形，

∴BM＝CF，NG＝AH，AN＝GH，MF＝BC＝2，

∵将线段EF绕点E逆时针旋转90°得到线段EG，

∴EG＝EF，∠GEF＝90°，

∴∠NEG+∠FEM＝90°，且∠NGE+∠NEG＝90°，

∴∠FEM＝∠NGE，且∠N＝∠FME＝90°，EF＝EG，

∴△EGN≌△EFM（AAS）

∴NE＝MF＝2，EM＝NG，

设AE＝CF＝a，

∴EM＝2﹣2a＝NG＝AH，AN＝2﹣a＝GH，

∴HD＝AD﹣AH＝2﹣（2﹣2a）＝2a，

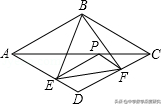
7．如图，在菱形ABCD中，AB＝6，∠ADC＝120°，P为对角线AC上的一点，过P作PE∥AB交AD与E，PF∥AD交CD于F，连接BE、BF、EF．

（1）求AC的长；

（2）求证：△BEF为等边三角形；

（3）四边形BEPF面积的最小值为_______．

【解析】本题考查了菱形的性质，平行四边形的判定和性质，等边三角形的判定和性质，三角形全等的判定和性质以及二次函数的性质，作出辅助线构建全等三角形是解题的关键．

（1）：连接BD，交AC于G，

∵菱形ABCD中，AC和BD是对角线，

∴BD⊥AC，AG＝CG＝1/2AC，

∵AB＝6，∠ADC＝120°，∴∠BAC＝∠BCA＝30°，

在Rt△ABG中，AG＝AB•cos∠BAC＝6×√3/2＝3√3，

∴AC＝2AG＝6√3；

（2）证明：∵在菱形ABCD中，AB＝6，∠ADC＝120°，

∴∠BAD＝∠BCD＝60°，∠ABD＝∠CBD＝∠ADB＝∠CDB＝60°，

∴△ABD是等边三角形，∴BD＝AB＝BC＝6，

∵PE∥AB，PF∥AD，

∴∠CPF＝∠CAD，四边形DEPF是平行四边形，∴ED＝PF，

∵AD＝DC，∴∠CAD＝∠ACD，∴∠CPF＝∠ACD，∴PF＝FC，

∴ED＝FC，∴易证明△BED≌△BFC（SAS），

∴BE＝BF，∠EBD＝∠FBC，

∵∠FBC+∠FBD＝∠CBD＝60°，

∴∠EBD+∠FBD＝∠EBF＝60°，∴△BEF是等边三角形；

（3）解：作PH⊥CD于H，

设FC＝x，则PF＝x，DF＝6﹣x，

∵∠ADC＝120°，PF∥AD，∴∠PFD＝60°，

在实际的解题中，如果求的是一条线段的最值或是几条线段和（或差）的最值，那么首选是尝试套用常见的基本的几何模型，若未能够直接套用几何模型，那么可以先分析题目中和动点有关的数量关系，特别是一些变化过程中的不变量，通过数量关系的转化，将其化归为常见的基本的几何模型（如将军饮马模型，胡不归模型，阿氏圆模型等），从而解决问题.若不能用几何模型求解，则可以寻找其中隐藏的函数关系，然后构建函数模型解决最值问题.