编辑|杪夏的光

在低密度条件下，高速旋转的转子在转子叶片翼型周围会产生一种特殊的低雷诺可压缩流，其中在层流分离剪切层上发生可压缩效应。与马赫数（M）的增加相关的可压缩效应和激波产生的情况以及由此引起的流场和空气动力学的变化趋势尚未被澄清。本研究旨在阐明可压缩效应及其对激波产生和流场的影响。

使用火星直升机"坚韧号"上所使用的CLF5605翼型进行二维非定常计算，采用计算流体力学（CFD）分析方法。计算条件设置为悬停时75%转子跨度处的雷诺数（Re=15,400），马赫数（M）从不可压缩（M=0.2）变化到跨音速（M=1.2）。采用由日本航空航天研究开发的可压缩流动求解器FaSTAR，并在多个条件下进行计算，其中扫过马赫数和攻角（α）。

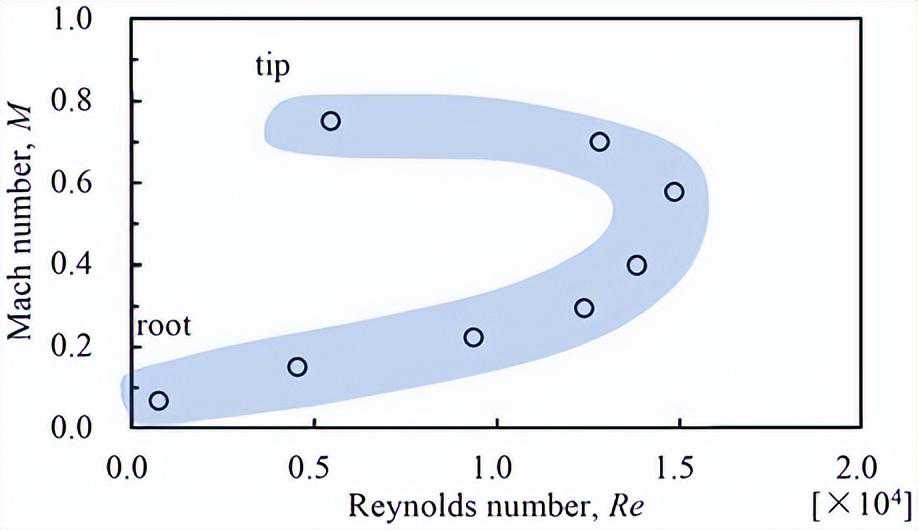
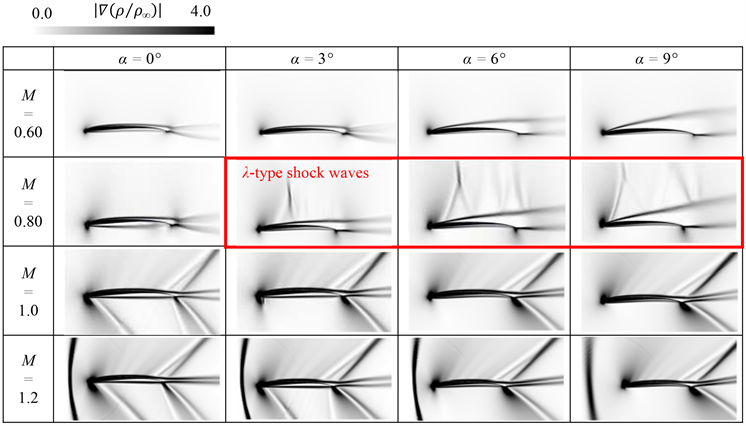
在M=1.0以上的流场类似于地球大气层，例如在前缘出现波阵面，而在M=0.80时，在α=3°以上分离剪切层上观察到多个λ型激波。在M=0.6和M=0.8之间的翼型周围Cp分布没有显着差异。从结果可以看出，多个λ型激波对翼型表面压力分布没有显著影响，而分离剪切层效应在表面压力变化和空气动力特性中起主导作用。

火星直升机（MH）已成为探索火星的新手段，与火星车任务相结合。火星直升机能够在火星表面复杂地形的影响下以相对较高的速度移动，这对于火星车来说是不可及的。与火星车的合作有望扩展其探测范围，获取以前难以探测的区域的详细和有意义的科学数据。

提出的火星直升机包括马里兰大学的火星自主旋翼车（MARV），主要由日本航空航天研究开发的用于火星撞击坑探测的六旋翼（HAMILTON），以及由美国国家航空航天局（NASA）喷气推进实验室（JPL）设计的"坚韧号"。"坚韧号"在2021年4月火星2020任务中完成了在地球以外行星上的首次成功动力飞行。

由于当前的"坚韧号"定位为技术验证器，它只具备近地表飞行的最低性能。特别是对于未来广泛区域的实用飞行探测，提高空气动力性能是实现增加有效载荷能力和延长巡航距离的关键技术挑战。

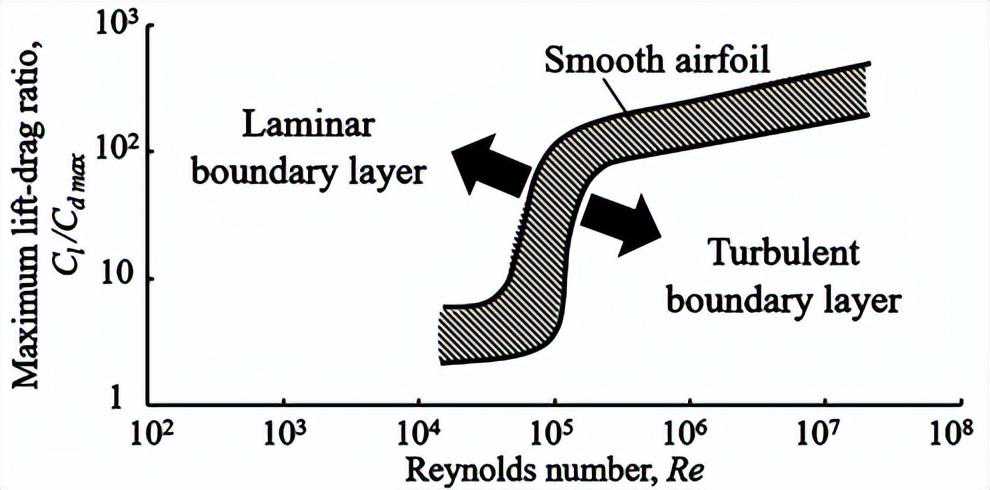
火星的重力约为地球的40%，大气密度约为地球的1%，这些特性使得火星对火星直升机来说是一个严酷的稀薄环境。火星的音速约为地球的70%，因为大气主要由二氧化碳组成，平均温度较低，约为223.2˚C。火星直升机旋翼叶片周围的雷诺数（Re）变得较低，约为O(10^3-10^4)，马赫数（M）接近M=0.80，激波更容易发生，特别是在叶片尖端附近。

显示了火星直升机旋翼叶片周围的流动条件。这种低雷诺数可压缩流是翼型气动设计的一个非常特殊的流动条件。已经有几项研究报告了这些特殊流动条件下翼型周围的流场情况。使用直接数值模拟（DNS）研究了低雷诺数区域圆柱体周围的可压缩效应。报告称，可压缩效应会延长尾流并导致轻微的分离延迟。

在东北大学的火星风洞中研究了Re=11,000时NACA0012-34翼型的可压缩效应。他们发现，在攻角大于α=7˚的高攻角范围内，升力系数随马赫数增加而减小。这是因为可压缩效应延迟了流动分离和层流-湍流转捩，阻止了层流分离泡的形成。研究了Re=6100和11,000时平板前缘层流分离泡的可压缩效应。

他们的结果显示，由于Kelvin-Helmholtz（KH）不稳定性引起的卷起分离剪切层受到可压缩效应的稳定，延迟了层流-湍流转捩和重新附着。该效应的大小在雷诺数较高时更为显著。这些研究仅局限于M=0.80或更低，部分原因是低雷诺数和跨音速风洞试验难以进行。

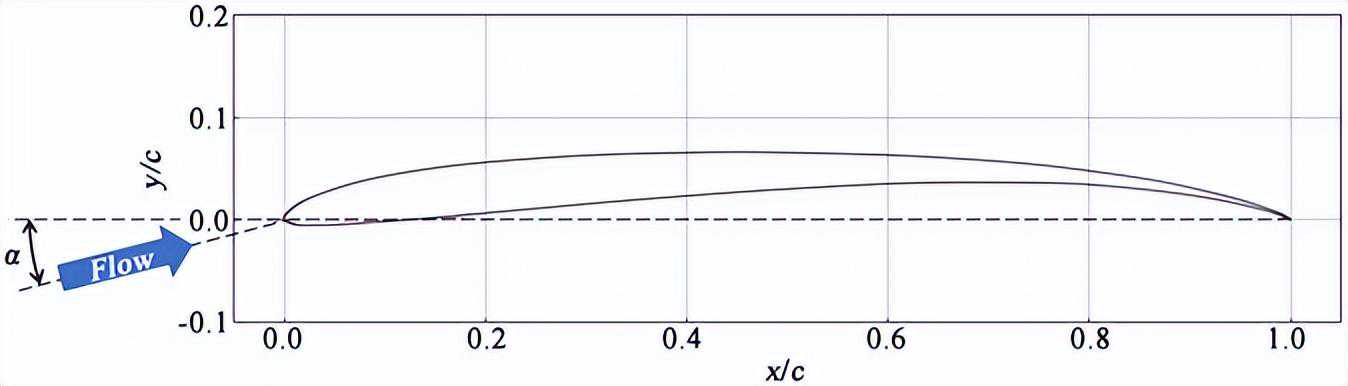
对于在火星直升机飞行雷诺数下的激波生成等跨音速速度的流场细节，仍然未知。Drela[13]对Re=200,000下Eppler387翼型周围的激波/边界层相互作用进行了数值研究，这比目标雷诺数高一个数量级。他成功地捕捉到了M=0.65时分离泡上方多个λ型激波的生成。这些相对较高的雷诺数对应于湍流边界层区域，不会出现层流分离。

由于边界层转捩，升阻比在Re=70,000以下急剧恶化（图2）。火星直升机飞行雷诺数下的流场预计将不同。通过使用CLF5605翼型对"坚韧号"三维旋翼叶片进行了CFD模拟，以研究激波生成的存在和影响。即使在翼尖处的高马赫数Mtip=0.90，火星大气中也不会产生激波，空气动力性能也不会受到损害。

这是因为前缘翼片产生的翼尖涡会产生绕叶片旋转的流动，从而降低了叶片周围的局部马赫数。尽管在他们的研究中，在Mtip=0.90以下的流场中没有观察到激波，但在未来火星直升机的实际操作中，可能需要以更高的旋转速度飞行，以增加有效载荷能力和延长巡航距离。

鉴于这些要求，对于流体结构的细节，如当产生激波时的层流分离泡/激波相互作用以及其对空气动力性能的影响，现有的基本认识还不足。通过使用CLF5605翼型，通过改变攻角和旋转速度（马赫数）从不可压缩速度到跨音速速度，描述了可压缩效应及其对流场和空气动力性能的影响。

研究使用CLF5605作为目标翼型，该翼型已被采用作为"坚韧号"火星直升机旋翼叶片的翼型。其几何形状如图3所示。CLF5605的特点是其薄度、小前缘半径和大翼弯度，在翼弦长（c）处的最大厚度比为5.0%，在x/c=0.20处的最大翼弯度比为4.9%。

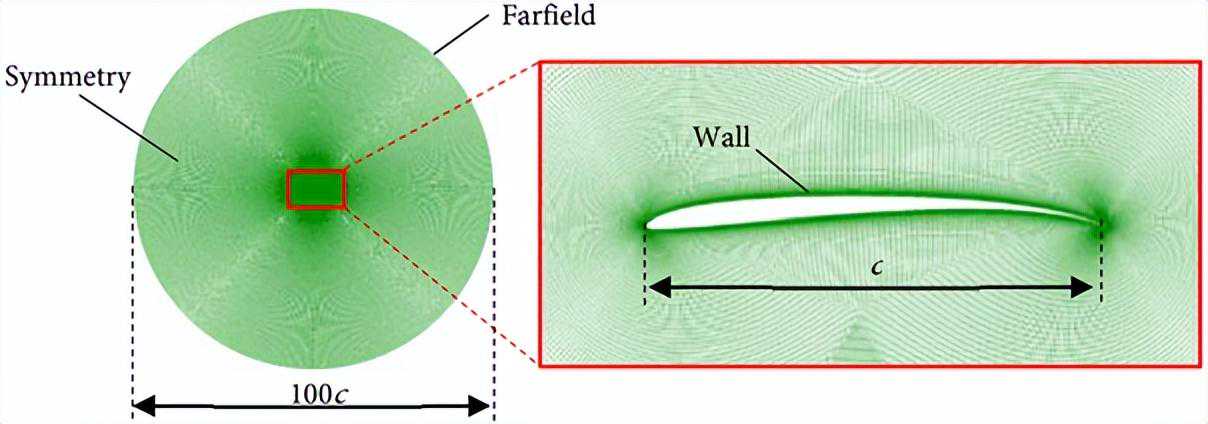
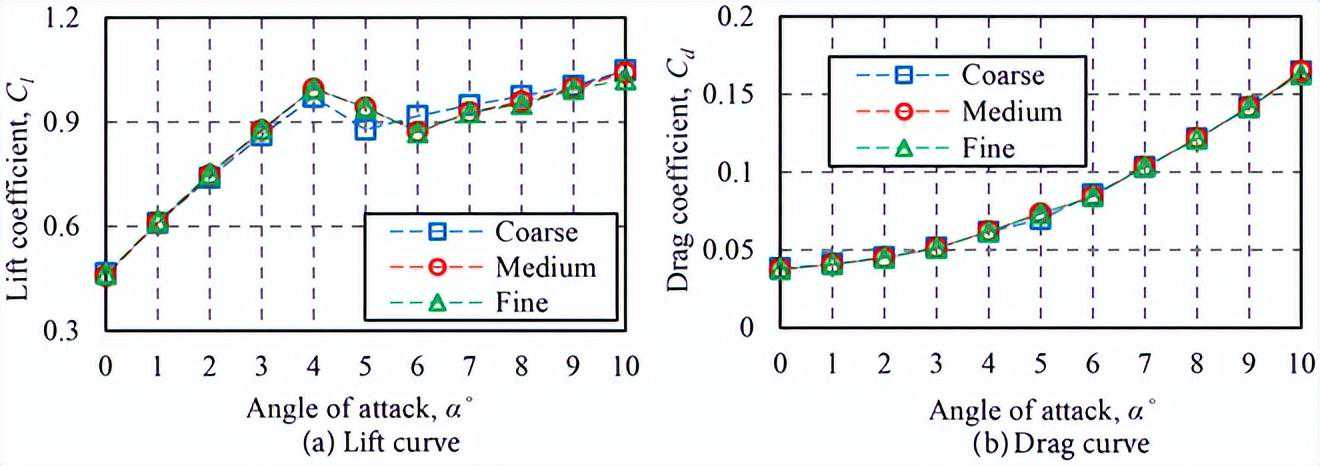
为了设计"坚韧号"火星直升机的旋翼叶片，通过CFD研究了CLF5605在Re=15,400和M=0.60下的二维（2D）流场。研究模拟了与"坚韧号"旋翼叶片等效弦长（r/R=0.75）相对应的流场。表2显示了设定的流动条件。研究的基本情况是Re=15,400和M=0.60，与Koning等人的CFD结果进行了验证比较。

目前并没有能够实现这些条件的风洞，进行风洞实验是困难的。通过数值计算进行了研究。需要注意的是，已经开发了可以实现接近表2中所示流动条件的低雷诺数可压缩流动的火星风洞。即使有这样一个专门用于火星大气飞行的特殊风洞，也很难将计算直接与实验结果进行比较，因为相关流动条件在操作范围之外。

通过将结果数值结果进行比较来评估其有效性。细节在第2.4小节中进行讨论。在低雷诺数区域，尤其是纯M效应对激波干涉的影响下，Re是固定的，只有M在变化。在保持Re=15,400的情况下，评估了M对流场和空气动力特性的影响。在实际的火星直升机操作中，随着旋转速度（马赫数）的变化，Re也会发生变化。

在基本情况下，密度和压力分别为ρ=1.24×10−3kg/m3和p=52.5Pa。根据流动条件，假定了（湍流）普朗特数与空气相同。Menterγ-Reθt作为过渡模型。在计算方法方面，采用了SLAU2计算无粘流量，因为SLAU2被证明对激波异常非常稳健，它可以在不改变方法的情况下系统地和高效地计算各种马赫数和攻角条件下的计算。

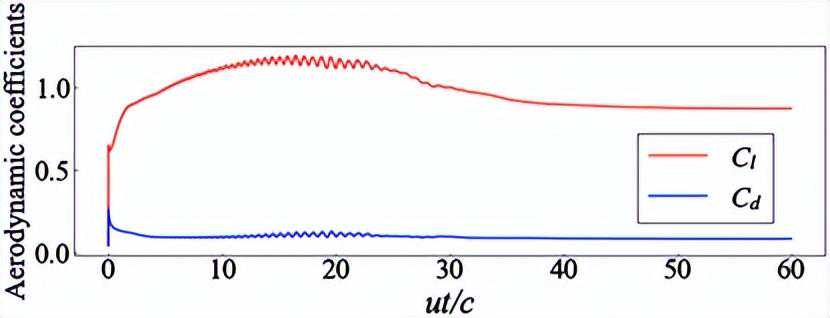
已经有报告称湍流模型和过渡模型对于捕捉翼型表面的层流分离泡（LSBs）是有效的。基于这些研究，研究采用了SA-AFT2017b湍流和过渡模型。在计算中，使用了中等网格（124,000个网格点），并进行了计算网格的收敛性验证。在图7中，显示了在无量纲时间为50至60的平均流场的风洞试验结果。

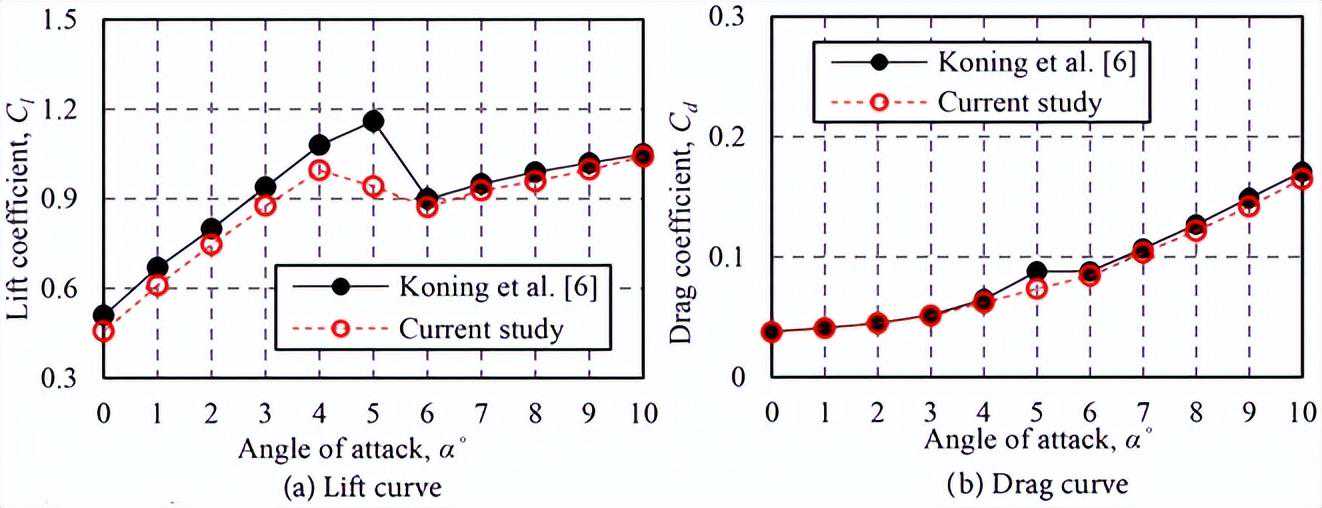
尽管在α=5˚和6˚处略有差异，但在每个网格水平上获得了类似的空气动力系数。特别是在α=5˚时，将中等网格和粗网格进行比较，升力系数和阻力系数的差异分别约为7%和5%。在所有攻角下，中等网格和细网格之间的升力和阻力系数的差异都小于2%。根据这个结果，判断中等网格收敛得足够好，因此中等网格（124,000个点）在所有计算中被使用。

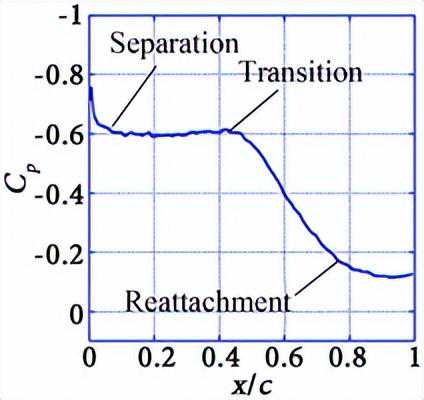
尽管在图8中在尾缘附近观察到了环流区域，但由于二维计算的原因，回流区域有些被高估。这些都可以归因于湍流模型对湍流转捩的依赖性。正如上面所述，是否在尾缘附近重新附着分离流动仍存在争议。根据基于Cp分布的过去研究结果，可以自然地假设在吸力面上发生了无重新附着的分离流动。

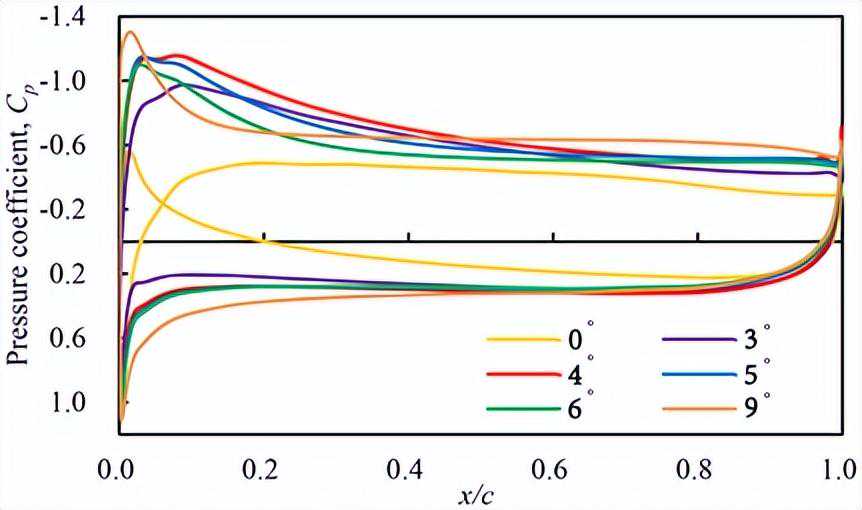
在这个假设的基础上，随着攻角的增加，可以发现从尾缘分离流向前缘分离流的逐渐转变。特别是在α=3˚和5˚之间，当分离点急剧向前移动时，在α=5˚或更大时，上表面大部分被分离流所覆盖。图5中在α=5˚处的Cl下降可以归因于前缘分离流的变化。

在α=4˚和6˚之间，尽管攻角改变后，吸力面和压力面上的Cp分布几乎没有变化，但在吸力面吸力峰值后的压力略有变化，Cl也有所下降。在α≥6˚时，吸力面上的负压增加，压力面上的正压也增加，导致Cl随着攻角的增加而增加。

在跨音速区域，对M=0.60到M=1.2的结果进行了比较，以评估激波对空气动力性能和流场的影响。图17显示了M=0.80到M=1.2之间的平均密度梯度场。可以确认，在M=1.0和M=1.2的所有攻角下都产生了激波。在M=1.0时，在尾缘处产生了一个尾激波，而在M=1.2时，在前缘前方观察到了一个鼻激波。

这些与在地球大气下的翼型典型流场非常相似。相比之下，在M=0.80以上α=3˚时，在CLF5605上方的分离剪切层上产生了多个λ型激波，这与所报道的Re=200,000时的激波结构非常相似。Drela描述了多个λ型激波生成机制如下：预压缩波与边界层分离并碰撞，导致预压缩波反射为膨胀波。结果产生了多个λ型激波。

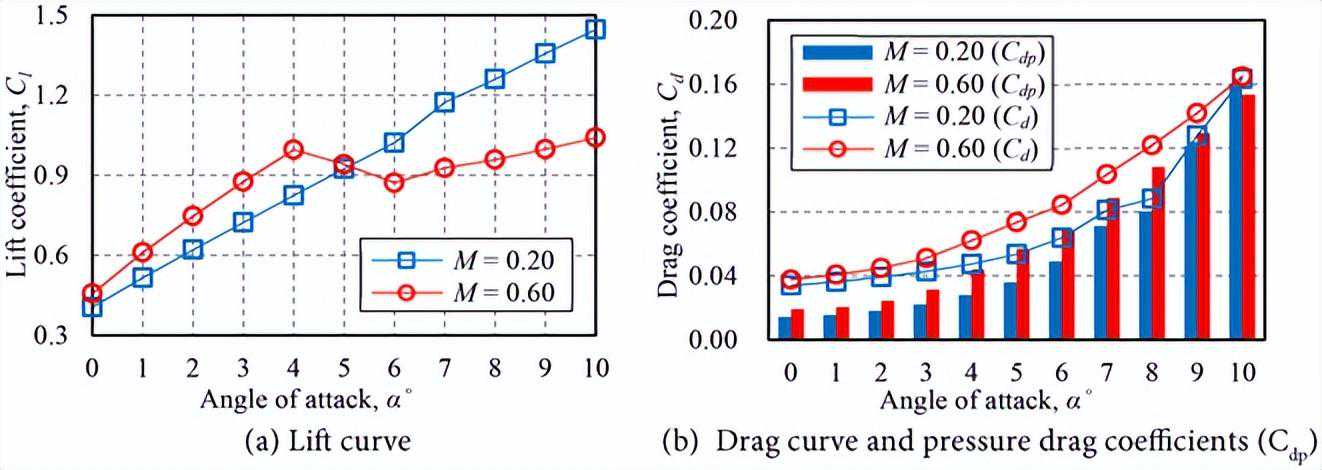
为了研究低雷诺可压缩流中火星直升机旋翼叶片的空气动力性能和流场，使用CLF5605翼型进行了二维非稳态模拟。评估了M对流场和空气动力性能的影响。比较M=0.20和M=0.60的结果表明，在M=0.60时，随着攻角超过α=7˚，由于压缩效应引起的分离层稳定，LSB消失。

这些现象在先前使用其他翼型进行的研究中已经报道过，研究中也发现了相同的现象。在M=0.80以上α=3˚时，吸力面上出现多个λ型激波。对于翼型表面的Cp分布，分离层的影响比λ型激波更为显著。对于M=1.0和M=1.2，在靠近前缘和尾缘附近的特征压力分布下，升力系数远小于M≤0.80的情况，尤其在低攻角（α=5˚以下）下，阻力系数在所有攻角下M=1.0时最大。