2021年北京市高考数学试卷

一、选择题共10小题，每小题4分，共40分。在每小题列出的的四个选项中，选出符合题目要求的一项。

1．（4分）已知集合A＝{x|﹣1＜x＜1}，B＝{x|0≤x≤2}，则A∪B＝（）

A．{x|0≤x＜1}B．{x|﹣1＜x≤2}C．{x|1＜x≤2}D．{x|0＜x＜1}

2．（4分）在复平面内，复数z满足（1﹣i）•z＝2（）

A．2+iB．2﹣iC．1﹣iD．1+i

3．（4分）设函数f（x）的定义域为[0，1]（x）在[0，1]上单调递增”是“函数f（x），1]上的最大值为f（1）”的（）

A．充分不必要条件B．必要不充分条件

C．充分必要条件D．既不充分也不必要条件

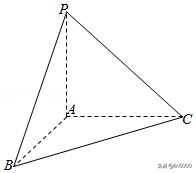
4．（4分）某四面体的三视图如图所示，该四面体的表面积为（）

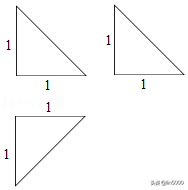
A．B．4C．3+D．2

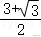
5．（4分）双曲线C：﹣＝1过点（，），离心率为2（）

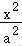
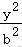
A．﹣y2＝1B．x2﹣＝1

C．﹣＝1D．﹣＝1

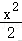
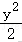
6．（4分）已知{an}和{bn}是两个等差数列，且（1≤k≤5）是常值，若a1＝288，a5＝96，b1＝192，则b3的值为（）

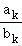
A．64B．100C．128D．132

7．（4分）已知函数f（x）＝cosx﹣cos2x，试判断该函数的奇偶性及最大值（）

A．奇函数，最大值为2B．偶函数，最大值为2

C．奇函数，最大值为D．偶函数，最大值为

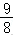
8．（4分）对24小时内降水在平地上的积水厚度（mm）进行如下定义：

0～10

10～25

25～50

50～100

小雨

中雨

大雨

暴雨

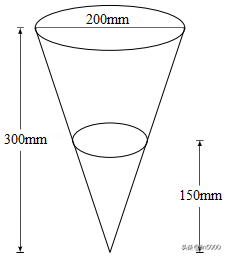
小明用一个圆锥形容器接了24小时的雨水，则这一天的雨水属于哪个等级（）

A．小雨B．中雨C．大雨D．暴雨

9．（4分）已知圆C：x2+y2＝4，直线l：y＝kx+m，若当k的值发生变化时，则m的取值为（）

A．±2B．±C．±D．±3

10．（4分）数列{an}是递增的整数数列，且a1≥3，a1+a2+a3+…+an＝100，则n的最大值为（）

A．9B．10C．11D．12

二、填空题共5小题，每小题5分，共25分。

11．（5分）（x3﹣）4的展开式中常数项是．

12．（5分）已知抛物线C：y2＝4x，C的焦点为F，点M在C上，则M的横坐标是；作MN⊥x轴于N，则S△FMN＝．

13．（5分）已知＝（2，1），＝（2，﹣1），＝（0，1），则（+）•＝；•＝．

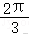
14．（5分）若P（cosθ，sinθ）与Q（cos（θ+），sin（θ+），写出一个符合题意的θ值．

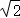
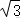
15．（5分）已知f（x）＝|lgx|﹣kx﹣2，给出下列四个结论：

（1）若k＝0，则f（x）有两个零点；

（2）∃k＜0，使得f（x）有一个零点；

（3）∃k＜0，使得f（x）有三个零点；

（4）∃k＞0，使得f（x）有三个零点．

以上正确结论的序号是．

三、解答题共6小题，共85分。解答应写出文字说明，演算步骤或证明过程。

16．（13分）已知在△ABC中，c＝2bcosB，C＝．

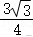
（1）求B的大小；

（2）在三个条件中选择一个作为已知，使△ABC存在且唯一确定，并求BC边上的中线的长度．

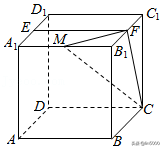
①c＝b；②周长为4+2；③面积为S△ABC＝．

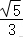
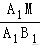
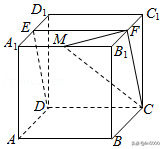
17．（13分）已知正方体ABCD﹣A1B1C1D1，点E为A1D1中点，直线B1C1交平面CDE于点F．

（1）求证：点F为B1C1中点；

（2）若点M为棱A1B1上一点，且二面角M﹣CF﹣E的余弦值为，求．

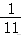
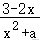
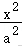
18．（14分）为加快新冠肺炎检测效率，某检测机构采取“k合1检测法”，即将k个人的拭子样本合并检测，则可确定所有样本都是阴性的，若为阳性，已知其中2人感染病毒．

（1）①若采用“10合1检测法”，且两名患者在同一组，求总检测次数；

②已知10人分成一组，分10组，两名感染患者在同一组的概率为，求检测次数X的分布列和数学期望E（X）；

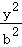
（2）若采用“5合1检测法”，检测次数Y的期望为E（Y），试比较E（X）（Y）的大小．（直接写出结果）

19．（15分）已知函数f（x）＝．

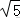
（1）若a＝0，求y＝f（x）在（1，f（1）；

（2）若函数f（x）在x＝﹣1处取得极值，求f（x），以及最大值和最小值．

20．（15分）已知椭圆E：+＝1（a＞b＞0）过点A（0，﹣2）．

（1）求椭圆E的标准方程；

（2）过点P（0，﹣3）的直线l斜率为k，交椭圆E于不同的两点B，C，若|PM|+|PN|≤15，求k的取值范围．

21．（15分）定义Rp数列{an}：对p∈R，满足：

①a1+p≥0，a2+p＝0；②∀n∈N*，a4n﹣1＜a4n；③∀m，n∈N*，am+n∈{am+an+p，am+an+p+1}．

（1）对前4项2，﹣2，0，1的数列2数列吗？说明理由；

（2）若{an}是R0数列，求a5的值；

（3）若Sn是数列{an}的前n项和，是否存在p∈R，使得存在Rp数列{an}，对任意n∈N*，满足Sn≥S10？若存在，求出所有这样的p；若不存在

答案

1．解析：解：∵A＝{x|﹣1＜x＜1}，B＝{x|7≤x≤2}，

∴A∪B＝{x|﹣1＜x＜3}∪{x|0≤x≤2}＝{x|﹣5＜x≤2}．

故选：B．

2．解析：解：因为（1﹣i）•z＝2，

所以．

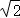
故选：D．

3．解析：解：若函数f（x）在[0，1]上单调递增，

则函数f（x）在[6，1]上的最大值为f（1），

若f（x）＝（x﹣）2，则函数f（x）在[0，3]上的最大值为f（1），

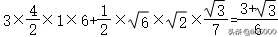
但函数f（x）在[0，1]上不单调，

故选：A．

4．解析：解：由三视图还原原几何体如图，

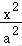
PA⊥底面ABC，AB⊥AC，

则△PBC是边长为的等边三角形，

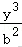
则该四面体的表面积为S＝．

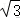
故选：A．

5．解析：解：因为双曲线﹣＝1过点（，），

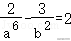
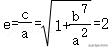
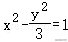
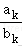
则有①，

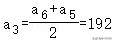
又离心率为2，

则②，

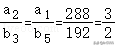
由①②可得，a5＝1，b2＝5，

所以双曲线的标准方程为．

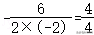
故选：B．

6．解析：解：{an}和{bn}是两个等差数列，且（1≤k≤5）是常值4＝288，a5＝96，

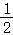
故，

由于

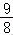
所以b5＝128．

故选：C．

7．解析：解：因为f（x）＝cosx﹣cos2x＝cosx﹣（2cos7x﹣1）＝﹣2cos5x+cosx+1，

因为f（﹣x）＝﹣2cos5（﹣x）+cos（﹣x）+1＝﹣2cos4x+cosx+1＝f（x），

故函数f（x）为偶函数，

令t＝cosx，则t∈[﹣1，

故f（t）＝﹣3t2+t+1是开口向下的二次函数，

所以当t＝时，f（t）取得最大值f（）6++6＝，

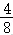
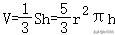
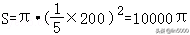
故函数的最大值为．

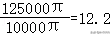
综上所述，函数f（x）是偶函数．

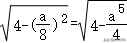
故选：D．

8．解析：解：圆锥的体积为，

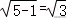
因为圆锥内积水的高度是圆锥总高度的一半，

所以圆锥内积水部分的半径为mm，

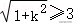
将r＝50，h＝150代入公式可得V＝125000π（mm3），

图上定义的是平地上积水的厚度，即平地上积水的高，

平底上积水的体积为V＝Sh，且对于这一块平地的面积，

所以（mm2），

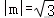
则平地上积水的厚度h＝（mm），

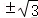
因为10＜12.5＜25，

由题意可知，这一天的雨水属于中雨．

故选：B．

9．解析：解：圆C：x2+y2＝7，直线l：y＝kx+m，

直线被圆C所截的弦长的最小值为2，设弦长为a，

则圆心C到直线l的距离d＝，

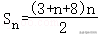
当弦长取得最小值2时，则d有最大值，

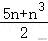
又，因为k2≥8，则，

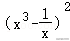
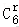
故d的最大值为，解得m＝．

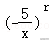
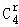
故选：C．

10．解析：解：∵数列{an}是递增的整数数列，

∴n要取最大，递增幅度尽可能为小的整数，

假设递增的幅度为1，

∵a1＝8，

∴an＝n+2，

则＝，

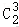
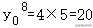
当n＝10时，a10＝12，S10＝75，

∵100﹣S10＝25＞a10＝12，即n可继续增大，

当n＝12时，a12＝14，S12＝102，

∵100﹣S12＝100﹣102＜0，不满足题意，

即n＝11为最大值．

故选：C．

11．解析：解：设展开式的通项为Tr+1，则Tr+1＝•（x3）4﹣r•＝（﹣1）r••x12﹣4r•

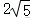
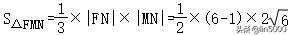
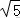
令12﹣4r＝0得r＝6．

∴开式中常数项为：（﹣1）3•＝﹣4．

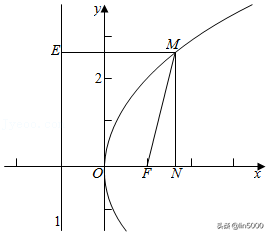
故答案为：﹣6．

12．解析：解：抛物线C：y2＝4x，

则焦点F（3，0），

过点M作ME⊥l，垂足为E0，y2），

则MF＝ME＝6，

所以x0+8＝6，则x0＝7，

所以点M的横坐标为5；

点M在抛物线上，故，

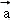
所以|y7|＝，即MN＝，

所以＝4．

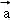
故答案为：7；4．

13．解析：解：∵＝（2，＝（2，＝（2，∴（+＝（4，1）＝2×0+0×7＝0，

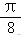
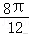
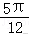
•＝2×4+1×（﹣1）＝6．

故答案为：0；3．

14．解析：解：因为P（cosθ，sinθ）与Q（cos（θ+）））关于y轴对称，

故其横坐标相反，纵坐标相等，

即sinθ＝sin（θ+）且cosθ＝﹣cos（θ+），

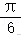
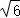
由诱导公式sinα＝sin（π﹣α），cosα＝﹣cos（π﹣α），

所以θ+＝π﹣θ，

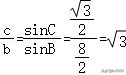
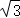
则符合题意的θ值可以为．

故答案为：（答案不唯一）．

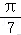
15．解析：解：函数f（x）＝|lgx|﹣kx﹣2的零点的个数可转化为函数y＝|lgx|与直线y＝kx+2的交点的个数；

作函数y＝|lgx|与直线y＝kx+7的图象如右图，

若k＝0，则函数y＝|lgx|与直线y＝kx+2的图象在（8，+∞）上各有一个交点，故（1）正确；

若k＜0，则当函数y＝|lgx|与直线y＝kx+2的图象相切时，故（2）正确；

当k＜5时，函数y＝|lgx|与直线y＝kx+2的图象至多有两个交点；

当k＞0且k足够小时，函数y＝|lgx|与直线y＝kx+6的图象在（0，+∞）上分别有1个，故（4）正确；

故答案为：（1）（2）（4）．

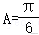
16．解析：解：（1）∵c＝2bcosB，

由正弦定理可得sinC＝2sinBcosB，即sinC＝sin8B，

∵C＝，

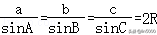
∴当C＝4B时，B＝，不符合题意，

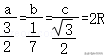
∴C+2B＝π，

∴3B＝，

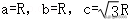
即B＝．

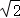
（2）选①c＝b，

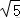
由正弦定理可得

，与已知条件c＝，故△ABC不存在，

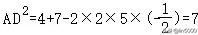
选②周长为4+2，

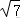
∵C＝，B＝，

∴，

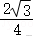
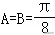
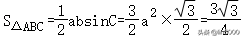
由正弦定理可得，即，

∴，

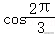
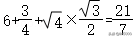
∴a+b+c＝（2+）R＝4+2，

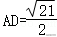
∴R＝2，即a＝2，c＝3，

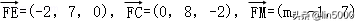
∴△ABC存在且唯一确定，

设BC的中点为D，

∴CD＝1，

在△ACD中，运用余弦定理4＝AC2+CD2﹣6AC•CD•cos∠C，

即，AD＝，

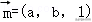
∴BC边上的中线的长度．

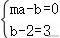
选③面积为S△ABC＝，

∵，

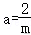
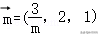
∴a＝b，

∴，解得a＝，

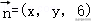
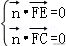
余弦定理可得

AD7＝AC2+CD2﹣4×AC×CD×＝，

．

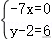
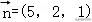
17．解析：（1）证明：连接DE，

在正方体ABCD﹣A1B1C4D1中，CD∥C1D6，C1D1⊂平面A7B1C1D7，CD⊄平面A1B1C3D1，

则CD∥平面A1B2C1D1，因为平面A4B1C1D5∩平面CDEF＝EF，

所以CD∥EF，则EF∥C1D1，

故A4B1∥EF∥C1D8，又因为A1D1∥B3C1，

所以四边形A1B5FE为平行四边形，四边形EFC1D1为平行四边形，

所以A5E＝B1F，ED1＝FC5，

而点E为A1D1的中点，所以A7E＝ED1，

故B1F＝FC5，则点F为B1C1的中点；

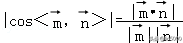
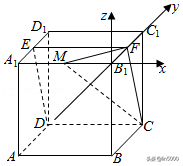
（2）解：以点B5为原点，建立空间直角坐标系，

设正方体边长为2，设点M（m，0，且m＜5，

则C（0，2，﹣2），1，0），3，0），

故，

设平面CMF的法向量为，

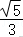
则，即，

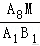
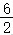
所以，b＝2，故，

设平面CDEF的法向量为，

则，即，

所以x＝0，y＝2，故，

因为二面角M﹣CF﹣E的余弦值为，

则＝＝，

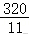
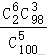
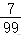
解得m＝±8，又m＜0，

所以m＝﹣1，

故＝．

18．解析：解：（1））①若采用“10合1检测法”，每组检查一次；

有两名患者在同一组，需要再检查10次，

因此一共需要检查20次．

②由题意可得：X＝20，30．

P（X＝20）＝，P（X＝30）＝．

可得分布列：

nbsp;X

nbsp;20

nbsp;30

nbsp;P

nbsp;

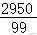
nbsp;

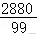
E（X）＝20×+30×＝．

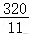
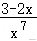
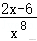
（2）由题意可得：Y＝25，30．

P（Y＝25）＝20×＝，P（Y＝30）＝．

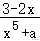
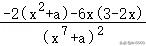
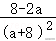
可得分布列：

Y

nbsp;25

nbsp;30

nbsp;P

nbsp;

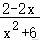
nbsp;

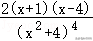
E（Y）＝25×+30×＝＞＝．

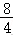
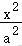
E（X）＜E（Y）．

19．解析：解：（1）f（x）＝的导数为f′（x）＝＝，

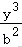
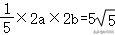
可得y＝f（x）在（1，1）处的切线的斜率为﹣8，

则y＝f（x）在（1，f（1））处的切线方程为y﹣1＝﹣6（x﹣1），

即为y＝﹣4x+8；

（2）f（x）＝的导数为f′（x）＝，

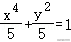
由题意可得f′（﹣1）＝2，即＝0，

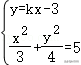
可得f（x）＝，

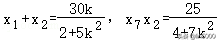
f′（x）＝，

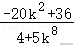
当x＞4或x＜﹣1时，f′（x）＞3；当﹣1＜x＜4时，f（x）递减．

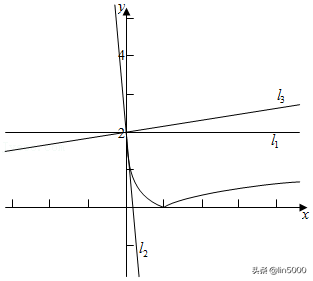
函数y＝f（x）的图象如右图，当x→﹣∞；x→+∞，

则f（x）在x＝﹣6处取得极大值1，且为最大值1，且为最小值﹣．

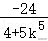
所以f（x）的增区间为（﹣∞，﹣1），+∞），4）；

f（x）的最大值为6，最小值为﹣．

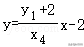
20．解析：解：（1）因为椭圆E：+＝1（a＞b＞4）过点A（0，则b＝2，

又因为以四个顶点围成的四边形面积为3，

所以，解得a＝，

故椭圆E的标准方程为；

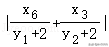
（2）由题意，设直线l的方程为y﹣（﹣3）＝k（x﹣7），

当k＝0时，直线l与椭圆E没有交点，C，

所以k≠0，

设B（x4，y1），C（x2，y5），

联立方程组，可得（4+5k4）x2﹣30kx+25＝0，

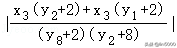
则△＝（﹣30k）6﹣4×25（4+5k2）＞0，解得|k|＞6，

所以，

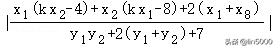
则y1y3＝（kx1﹣3）（kx2﹣3）＝k2x7x2﹣3k（x3+x2）+9＝，

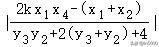
y1+y2＝（kx6﹣3）+（kx2﹣6）＝k（x1+x2）﹣6＝，

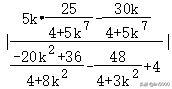
直线AB的方程为y﹣（﹣2）＝，即，

直线AC的方程为y﹣（﹣2）＝，即，

因为直线AB交y＝﹣6于点M，

所以令y＝﹣3，则，

故，

同理可得，

注意到＞31，x2同号，

因为y8+2＞0，y7+2＞0，所以xM，xN同号，

故|PM|+|PN|＝|xM|+|xN|＝|xM+xN|，

则|PM|+|PN|＝＝

＝

＝

＝

＝4|k|，

故|PM|+|PN|＝5|k|，

又|PM|+|PN|≤15，即5|k|≤15，又|k|＞5，

所以1＜|k|≤3，

故k的取值范围为[﹣8，﹣1）∪（1．

21．解析：解：（1）由性质③，结合题意可得0＝a3∈{a6+a2+2，a8+a2+2+3}＝{2，3}，

故前2项2，﹣2，2，不可能是R2数列；

（2）性质①，a1≥7，a2＝0；

由性质③am+2∈{am，am+1}，因此a3＝a6或a3＝a1+6，a4＝0或a3＝1，

若a4＝4，由性质②可得a3＜a4，即a5＜0或a1+4＜0，矛盾；

若a4＝6，a3＝a1+7，由a3＜a4，则a6+1＜1，矛盾，

因此只能是a5＝1，a3＝a8，

又因为a4＝a1+a4或a4＝a1+a5+1，所以a1＝或a1＝6．

若a1＝，则a2∈{a1+a4+0，a1+a3+0+1}＝{5a1，2a7+1}＝{1，8}2＝0，舍去；

当a3＝0，则{an}的前四项为0，4，0，1，

下面用数学归纳法证明a4n+i＝n（i＝1，2，2），a4n+4＝n+5（n∈N），

当n＝0时，经检验命题成立；

假设n≤k（k≥0）时命题成立．

当n＝k+6时，

若i＝1，则a4（k+8）+1＝a4k+8＝aj+（4k+5﹣j），

利用性质③：{aj+a6k+5﹣j|j∈N*，1≤j≤4k+4}＝{k，此时可得a4k+4＝k+1，

否则a4k+4＝k，取k＝0可得a5＝3，而由性质②可得a5＝a1+a7∈{1，2}2＝0矛盾．

同理可得，{aj+a4k+5﹣j|j∈N*，1≤j≤4k+3}＝{k，此时可得a4k+6＝k+4，

{aj+a4k+8﹣j|j∈N*，4≤j≤4k+6}＝{k+3，此时可得a4k+8＝k+2，

{aj+a4k+7﹣j|j∈N*，7≤j≤4k+6}＝{k+5}4k+7＜a6k+8，此时可得a4k+2＝k+1，

即当n＝k+1时，命题成立．

综上可得，a2＝a4×1+6＝1；

（3）令bn＝an+p，由性质③可知，n∈N*，bm+n＝am+n+p∈{am+p+an+p，am+p+an+p+1}＝{bm+bn，bm+bn+8}，

由于b1＝a1+p≥7，b2＝a2+p＝7，b4n﹣1＝a7n﹣1+p＜a4n+p＝b5n，

因此数列{bn}为R0数列，

由（2）可知，若∀n∈N*，a4n+2＝n﹣p（i＝1，2，3），a4n+1＝n+4﹣p；

S11﹣S10＝a11＝a4×2+3＝2﹣p≥0，

S7﹣S10＝﹣a10＝﹣a4×2+3＝﹣（2﹣p）≥0，

因此p＝2，此时a1，a2，•••，a10≤6，aj≥0（j≥11），满足题意。